[백준] 1934번 : 최소공배수(유클리드 호제법)- 파이썬[Python]

문제

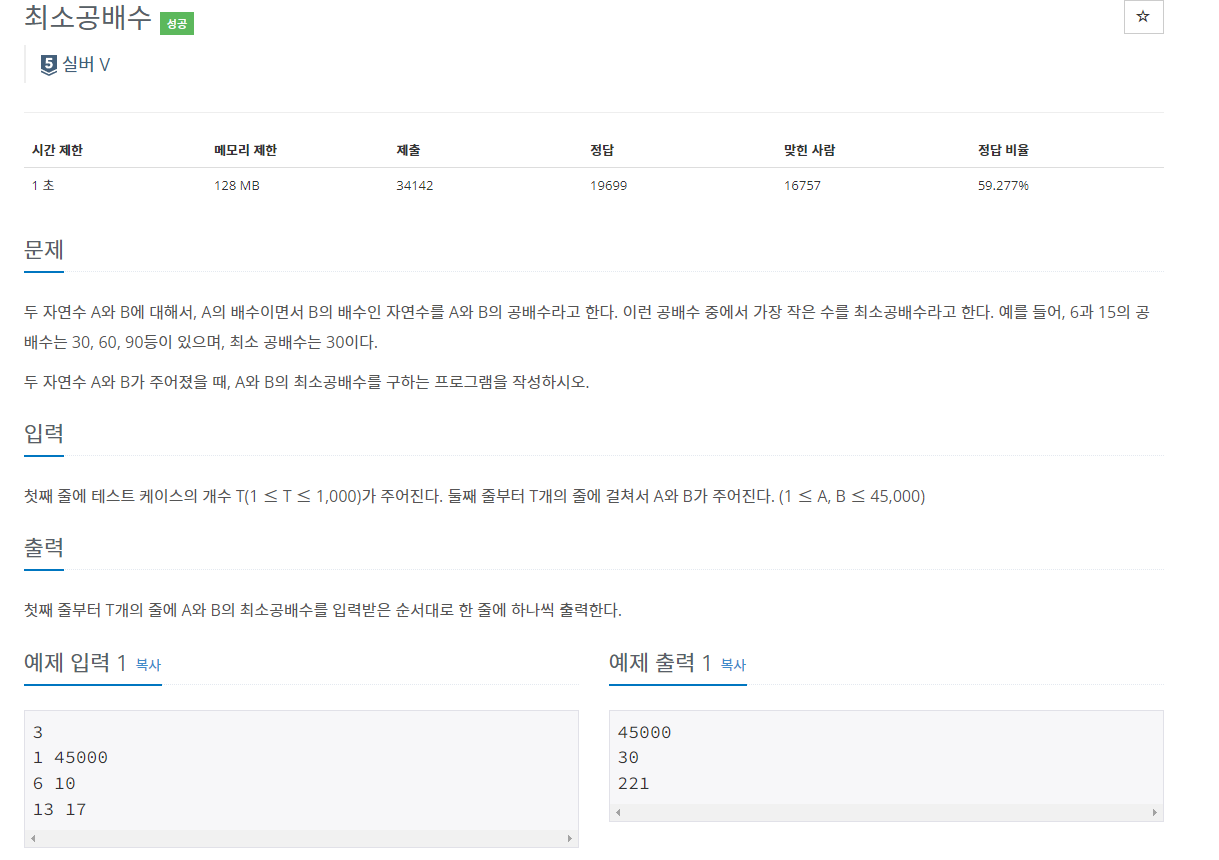
1934번: 최소공배수

 

 

 

 

풀이

 

출처 : https://jwj4519.com/

 

 

처음에는 위 공식과 같이

초등학교때 배웠던 최소 공배수를 구하는 공식으로 코드를 짰었지만

 

 

T=int(input())
c=[]
def multiply(arr):
  ans = 1
  for n in arr:
    ans *= n
  return ans

for i in range(T):
  A = list(map(int,input().split()))
  n = 2
  if A[0]==1 or A[1]==1: #한 쪽 수가 1일 경우
    print(max(A))
    continue
  while n <= max(A):
    if (A[0]%n==0) and (A[1]%n)==0:
      c.append(n)
      A[0]=A[0]/n
      A[1]=A[1]/n
      n=2
    else:
      n+=1
  print(int(multiply(c)*A[0]*A[1]))

코드가 너무 복잡하고 값이 나오긴 하는데 초과출력의 문제와

입력값이 너무 커지면 시간이 오래걸리는 문제에 봉착했다.

 

유클리드 호제법

출처 : https://j1w2k3.tistory.com/1173

 

시행착오 끝에

이 문제는 유클리드 호제법을 활용해서 푸는 문제임을 알게 되었다.

양수의 나머지의 나머지를 계속 연산하여

나머지가 0이 되었을때 작은 수가 최대공약수 이며

기존 두 수를 곱한 값을 최대공약수로 나눈값이 최소 공배수이다. 

 

T=int(input())

for i in range(T):
  A,B = map(int,input().split())
  a=A
  b=B
  n=1
  while n!=0:
    n=a%b
    a=b
    b=n
    
  print(int(A*B/a))

위에서 짠 코드와 비교했을때

훨씬 간단해 진 것을 볼 수 있다.

알고리즘 문제를 풀때 기존 상식으로 코드를 구현하는 경험도 필요하지만,

문제를 좀 더 효율적으로 풀 수 있는 알고리즘 학습의 중요성을 깨달았다.